Working Theory Of A Half Wave Rectifier Circuit | Waveform | Mathematical Analysis
A half-wave rectifier is a type of rectifier that converts alternating current (AC) into direct current (DC) by allowing the current to pass through it in only one direction during each cycle of the AC supply. This means that it only utilizes one half-cycle of the AC waveform, either the positive or the negative half, and blocks the other half. As a result, the output is a series of pulses, rather than a smooth and continuous flow of DC current.
The simplest half-wave rectifier consists of a single diode connected in series with the AC supply and the load. When the AC voltage is positive, the diode becomes forward-biased and allows current to flow through to the load. When the AC voltage is negative, the diode becomes reverse-biased and blocks current from flowing, resulting in no output during the negative half-cycle.
Due to its simplicity, the half-wave rectifier is easy to understand and inexpensive to build. However, its efficiency is relatively low, and it produces a lot of ripple in the output DC signal. This ripple can be somewhat mitigated with the use of filtering components, such as capacitors, but the half-wave rectifier is still generally less preferred for applications requiring a smooth and stable DC supply. It is most suitable for low-power applications where cost and complexity are major considerations.
Circuit Diagram
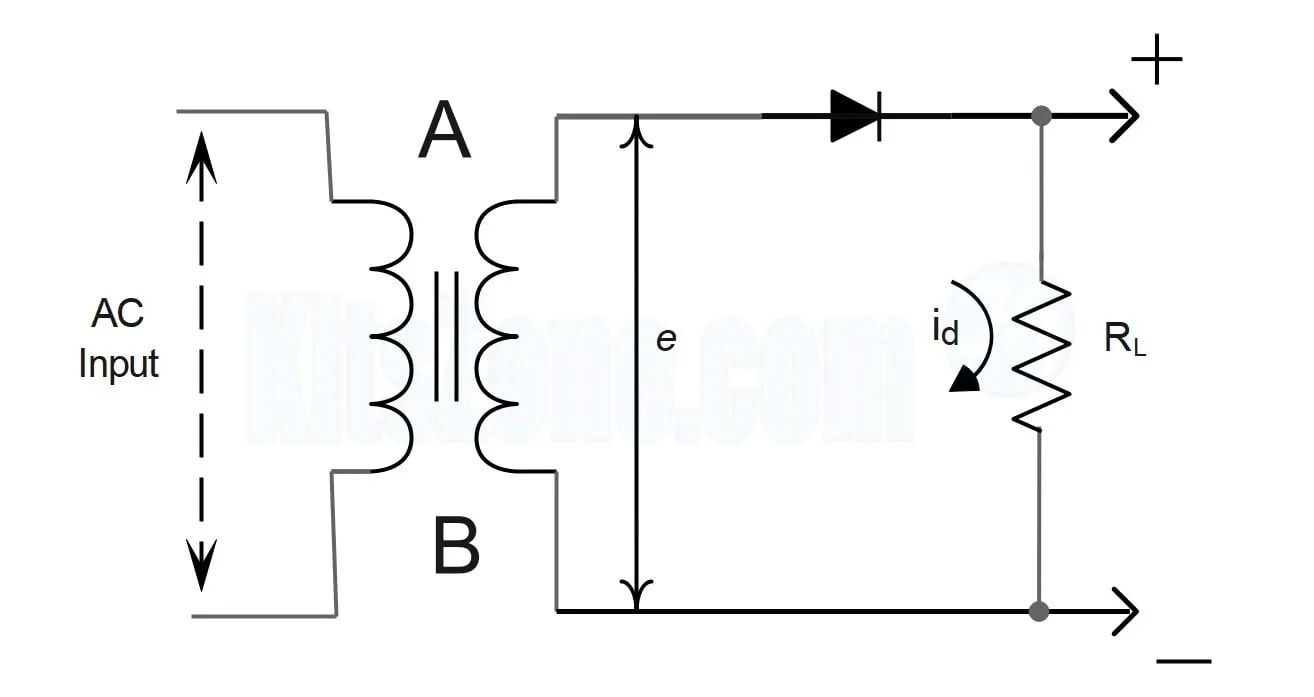
Circuit Details
In the circuit presented above, a single diode functions as a half-wave rectifier. The to-be-rectified AC supply is connected in series with the PN junction diode and a load resistance RL. In this experiment, the AC supply is obtained through a transformer. The use of transformer offers two benefits.
First, it allows us to increase or decrease the AC voltage depending on the circumstances using a step up or step down transformer.
The transformer also isolates the rectifier circuit from the power line, reducing the risk of electric shock.
Circuit Working
A is positive with respect to B when an AC supply is applied to the input circuit during one half of the cycle. This makes the diode's P terminal positive with respect to its N terminal. Consequently, the diode is forward biased, and current travels through the load RL in the direction depicted in the circuit above. During the subsequent half-cycle, the point A is negative relative to point B. Consequently, the diode is reverse biased and does not conduct (except for a very small reverse current which is negligible), so no current flows through the load RL.
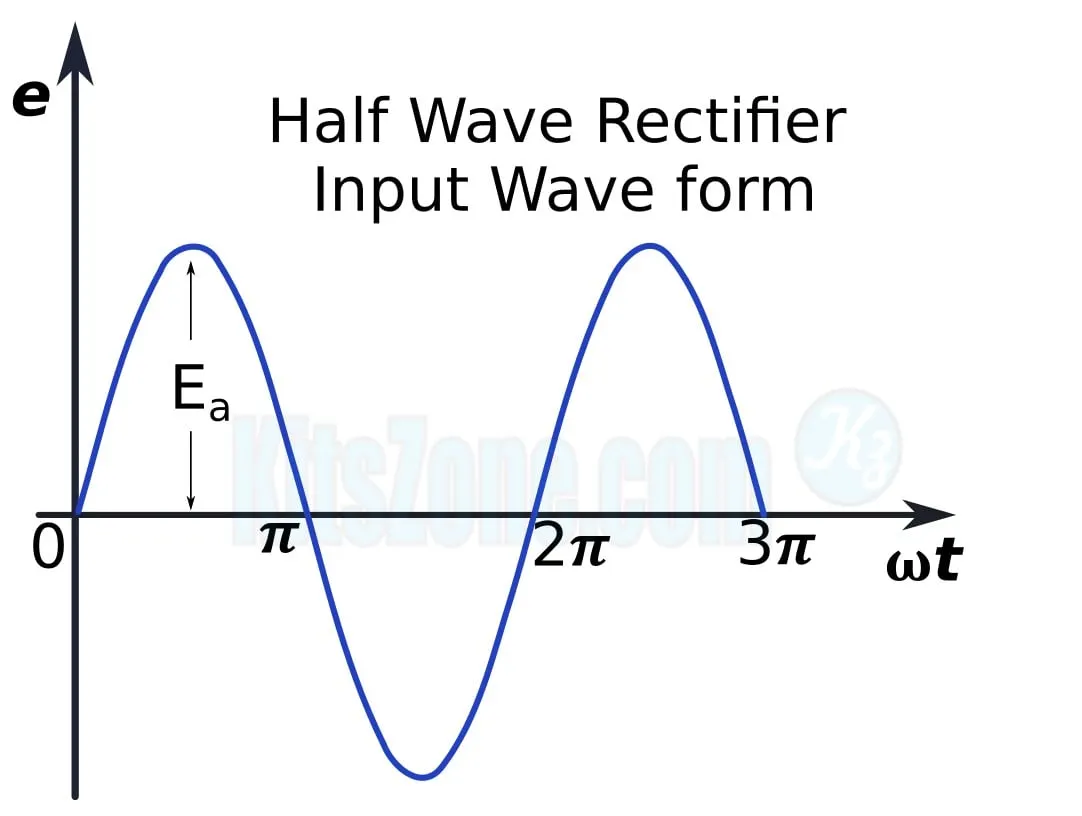
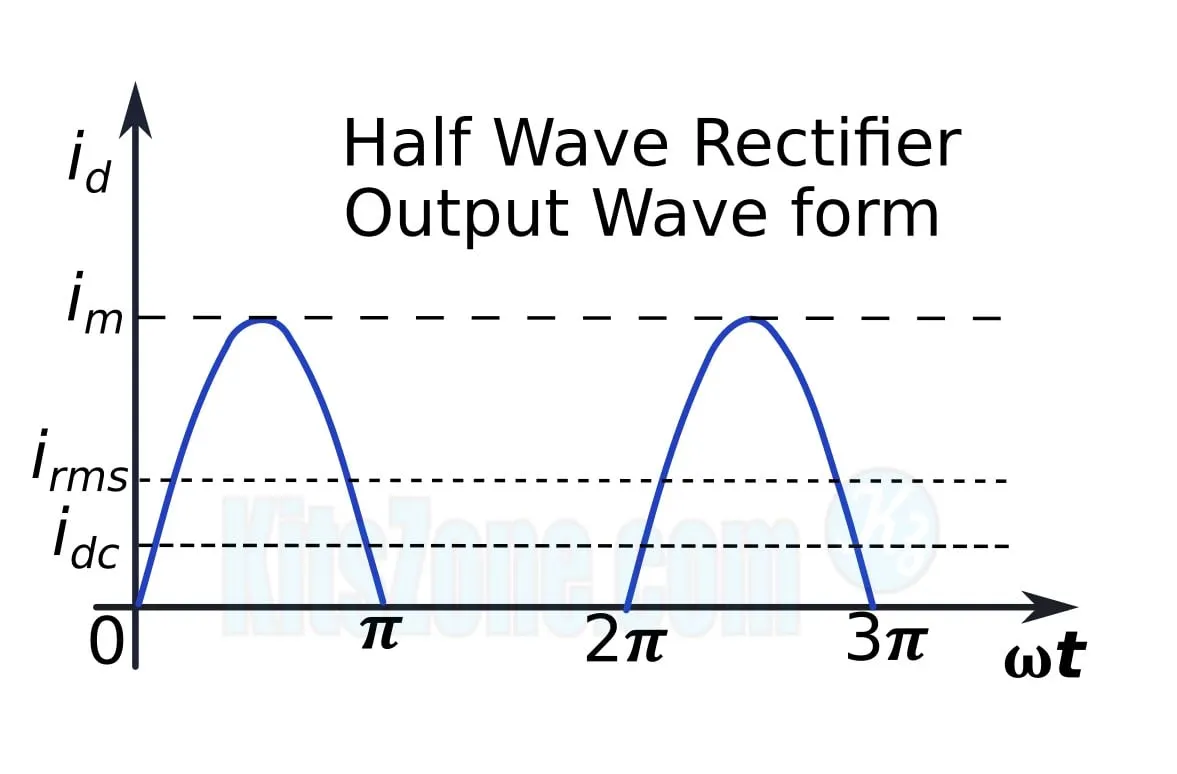
The diode conducts during the positive half cycle and does not conduct during the negative half cycle. Thus, when an AC signal is applied to the input of the rectifier, only one-directional current flows through RL. The output across RL will therefore be a DC. The wave forms of the input and output are shown below. As the output comprises only the positive half of the input wave, this rectifier is referred to as a half-wave rectifier.
Input And Output Waveform
Mathematical Analysis
Let e = E0 + sin wt be the input voltage to the rectifier, where E0 be the peak input voltage. When the diode is conducting, let id be the current flowing through the circuit and let the voltage drop across the diode be ed.
Assuming the ohmic resistance of the secondary of the transformer as negligible and applying Kirchhoff's voltage law to this circuit we have,
$$\eqalign{
& e = {e_d} + {I_d}{R_L} \cr
& = {i_d}{R_f} + {I_d}R \cr} $$
Where Rf is the forward dynamic resistance of the diode.
$$\eqalign{
& \therefore e = {I_d}\left( {{R_f} + {R_L}} \right) \cr
& i.e.,{E_o}\sin \omega t = {I_d}\left( {{R_f} + {R_L}} \right) \cr
& i.e.,{i_d} = {i_m}\sin \omega t \cr} $$
where ${i_m} = {{{E_o}} \over {{R_f} + {R_L}}}$ is the peak current.
If the resistance of the diode is negligible compared to RL, then
$${i_m} = {{{E_o}} \over {{R_L}}}$$
For a half wave rectifier, we have, (Refer the second graph)
DC Value Of Current(Idc)
From the second graph, it can be noticed that the output current is not steady but contains fluctuations despite of being a DC current. The average value of this fluctuating DC current can be calculated as follows: